What does "enharmonic spelling of a note" mean?
Enharmonic spelling is when the same sounding pitch is spelled in different note names. For instance, F♯ and G♭ are the exact same notes when they are played with a fixed pitch instrument like the piano, but they are spelled differently.
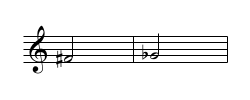
♯, ♭, does it matter?
You are playing a piece, and you encounter an F♯. You keep playing, and now you see a G♭. You wonder "Why are they not both F♯? I like '♯' better than '♭', can't they be all '♯' to make it simpler?"
This article will explore reasons why enharmonic spelling exists, and why they make sense.
General rules of when to use sharps and flats
When you decide whether to use a sharp or flat, there are some things you need to consider:
Key and key signatures
Scales and chords
Sharps to go up, flats to go down
See if you can justify the augmented or diminished intervals created by accidentals
Let's take a look at each rule more in depth.
Key and key signatures
The first rule we should know has everything to do with the key and key signatures. You will see more ♯s in a key based on ♯s such as G major, A major, and C♯ minor. On the contrary, you would see more ♭s in a key based on ♭s such as Bb major, Db major, and Eb minor.
Take the key of G major and G♭ major for instance. If you wanted to raise the 4th note of the scale by half a step, you would write a C♯ in G major, while it would be a C♮ in G♭ major.


What if you wanted to lower the 6th note of the scale? You would write a E♭ in G major, but it would be a E♭♭ in G♭ major.
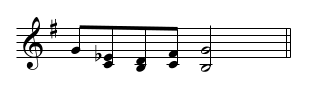

Scales and chords
Scales
The excerpts below are from the Gavotta of Symphony No.1 by Prokofiev.

Do we really need to spell it with an F double sharp and a B sharp? Let's compare the 1st and the 3rd measures to figure it out.

The first measure makes perfect sense. The first note, D goes down to a C♯ and comes back (this C♯ is called a neighboring tone). Then the notes go up in scale.
The 3rd measure takes on the exact same concept of scales as the 1st measure, which ends up with an F double sharp and a B sharp.
Let's edit the original. In the 3rd measure, what if we decided to use a G♮ and C♮ instead. Then the music should look like this:

As you see, now the sense of scale is broken, and it introduces an interval of a diminished 3rd. These notes no longer serve any musical purpose. When you try to sing the first measure you will find it much more difficult in our "edited" version than the original.
Chords
There are times when chords affect the accidentals. Look at the excerpt below from Preludes by Debussy.


This piece is in G♭ major but it is in E♭ major temporarily. There is a C♭ at the end of the first measure, which makes a C♭ major chord. Then, the chords ascend by a whole step at each 8th note, from C♭ major to D♭ major to E♭ minor.
This chord progression would not happen if the C♭ were spelled with B♮ as you can see in the second example. Now there is a strange chord with E♭, G♭, and B♮, which does not serve any musical purpose and has no musical connection to the chords before and after.
Sharps to go up, flats to go down
Because a sharp will raise a note by a half step, it has a tendency to move upward, whereas a flat has a tendency to move downward because it lowers a note by a half step. Please note this is a highly generalized rule, and you will find many exceptions. Nonetheless, knowing this rule will help you understand one of the purposes of ♯s and ♭s.
Take a look at these examples from Serenade by R. Fuchs


The first example is the composer's original. The second example has an A♯ instead of a B♭. It is not the end of the world to spell this passage with an A♯. However, all the notes are going down from one to the next, and a ♭ has a tendency to go downward, so a B♭ would be a preferred choice.
Now you might ask "Then why is there a C♯ instead of a D♭. All the notes are descending so wouldn't a D♭ be more appropriate?" The answer is: "C♯ is more appropriate", and here is why.
When you look at the original notes by the composer, you will notice that this is a descending scale. When you take out the B♭, you are left with:

If you spelled it with a D♭, it will look like:

Do you see how this breaks the line of a scale? Instead of every note descending one by one, now there is a jump from a D to a B. In addition to that, the interval of D♭ to B♮ is a diminished 3rd, which would make the scale even more jerky. C♯ is a much smoother and more natural way to handle this passage.
Let's take a look at another example.

You will notice that everything is the same except for the 3rd note. The one on the left is spelled with an E# while the one on the right is spelled with an F♮. Even though we could spell it either way, E# is a better choice, and here is why.
The 2nd note is a C#. When you go to an E# after that, the interval is a major 3rd. In comparison, if you go to an F♮, it is a diminished 4th. It is easier to guess an interval of a major 3rd than a diminished 4th.
This is a broken F# minor chord, and the notes are going up, which means there is an upward motion on these notes. A '#' has a stronger tendency to go upward than a '♮'. When it is spelled with an E#, the chord gains an extra push going upward from the E# because this is as if the E# was supposed to be an F# but it couldn't quite make it. E# holds a meaning, serves a purpose, and it does not get in the way of the F# sharp minor chord. In comparison, when it is spelled with an F♮, it does not serve any musical purpose. It stands alone with no significant correlation with the surrounding notes. In addition, it gets in the way of F# minor because of the minor 2nd clash between the F♮ and F#.
See if you can justify the augmented or diminished intervals created by accidentals
Take a look at these examples from Prokofiev.


This is taken from the 1st movement of Symphony No.1. The first example is the original by the composer, which creates a diminished 4th between the A♯ and D. In the second example, the A♯ has been changed to a B♭. As a result, the interval of the two notes is a major 3rd. Does that mean the second example is better than the first?
Please look at the examples below. I have picked out the main notes of the passage to have a clearer vision of the notes.

You can see that the F♯ moves to the A♯ which acts as a temporary leading tone to the B. The A♯ serves a musical purpose, and it is rather easy to hear the notes in your head. Compare that to the next example.

All of a sudden the B♭ loses any musical meaning in the context of the phrase. It does not belong anywhere, it just stands alone. Also, now the B♭ is creating a diminished 4th against the F♯, which makes it difficult to hear the notes in your head.
When you look at them this way, it becomes clear that an A♯ is a better choice than a B♭ in this particular case even though the A♯ creates a diminished interval against the D.
Let's look at one more example.

This is from the 1st movement of Serenade for Strings by Elgar. The F double sharp creates a diminished 3rd with the previous note, 'A'. Would it be better if the F double sharp were a G♮?
The F double sharp is an ornamental note. Without it the music should look like this, and it functions just fine.

The purpose of the F double sharp is to give an extra push to the G♯ on the next measure. The music gains more direction with the F double sharp because sharps have a tendency to move upward afterwards. So this could be spelled with a G♮ but, musically speaking it makes better sense with the F double sharp.
After all these examples, I hope you can start to understand the necessity of notes like B♯s and A♭♭s. They look strange at first, but once you understand the reason they will actually help you play more in tune, and help you play more musically.