Perfect intervals
Now we know all about major and minor intervals, let's talk about perfect intervals. Unison, 4th, 5th, and octave are perfect intervals. They are called perfect because of the way they sound together. It is a little bit difficult to explain in words, but basically, perfect intervals sound pure and simple when they are in tune. The major and minor intervals create a significant amount of clash between the two notes. This clash makes these intervals sound rich but at the same time they are not as pure as the perfect intervals. You will be able to tell the difference once you play them and listen for the differences between the perfect and the other intervals.
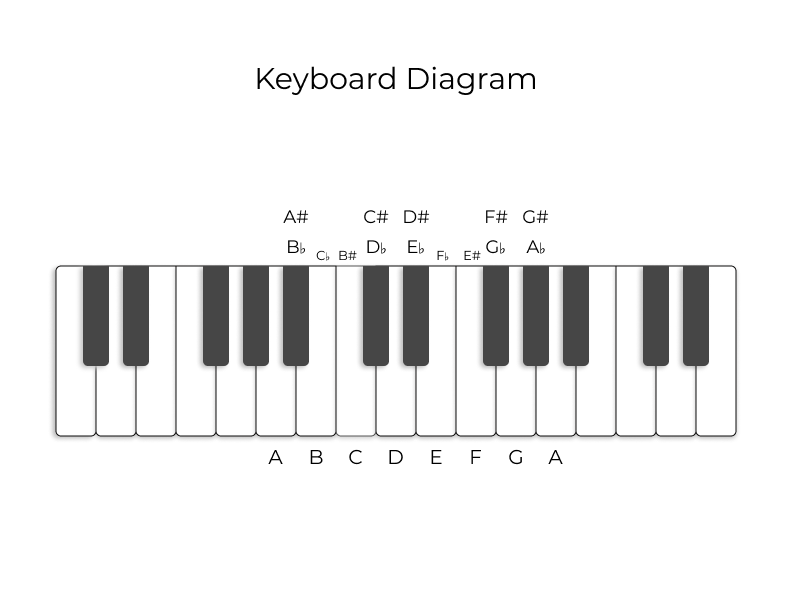
As in the previous articles, I am attaching a diagram of a keyboard for your reference.
Unison and octave
Even though unison and octave are perfect intervals, we don't say 'perfect unison', or 'perfect octave'. We simply say 'unison' or 'octave'.
An unison is the two notes that are exactly the same. A♮ and A♮ would be an unison.

An octave is the two notes that are the same (A♮ and A♮ for instance) but they are apart by 7 notes. For instance, play an A♮, and find another A♮ that is 7 notes higher or lower, then you just played an octave.

Perfect 4th
Intervals such as A to D, and F to B♭ are perfect 4ths. You can think of the distance of a perfect 4th as a major 3rd plus a half step, or you can count 5 half steps. Also, it is good to know that the open strings of the double bass are tuned in perfect 4th.
I find it helpful to think of the interval on a fingerboard. Let's think of the C on the G string. A perfect 4th above the C is the F on the D string. How would you play the two notes? You would place the two fingers with a distance of a whole step apart on two strings. It is like when you figured out the 6th on the fingerboard, but the order of the fingers are backwards now.

Another way to think about the 4ths on the fingerboard is as follows. Think about playing a note from the 1st finger to a 4th finger on one string with our regular hand frame. That's a perfect 4th. Let's say we play an E on the D string with the 1st finger, then play an A on the same string with the 4th finger. we are not contracting or expanding our hand, this is our normal hand frame, and that would produce an interval of perfect 4th.
Perfect 5th
You might know the fact that the open strings of the violin, viola, and cello are tuned in perfect 5th! Just think of open strings next to each other, and they are always perfect 5th. And that means if you would put one finger across two strings, the interval of the two notes is a perfect 5th. I definitely recommend thinking of a fingerboard when you figure out a 5th.

Flipping of the intervals
You've learned quite a bit about intervals. Now, let's talk about how intervals are related to each other when they are flipped. You will feel really confident about intervals once you understand it. Also, you will have a much easier time figuring out large intervals.
Look at the diagram below. Here is a PDF version if you would like to download it.
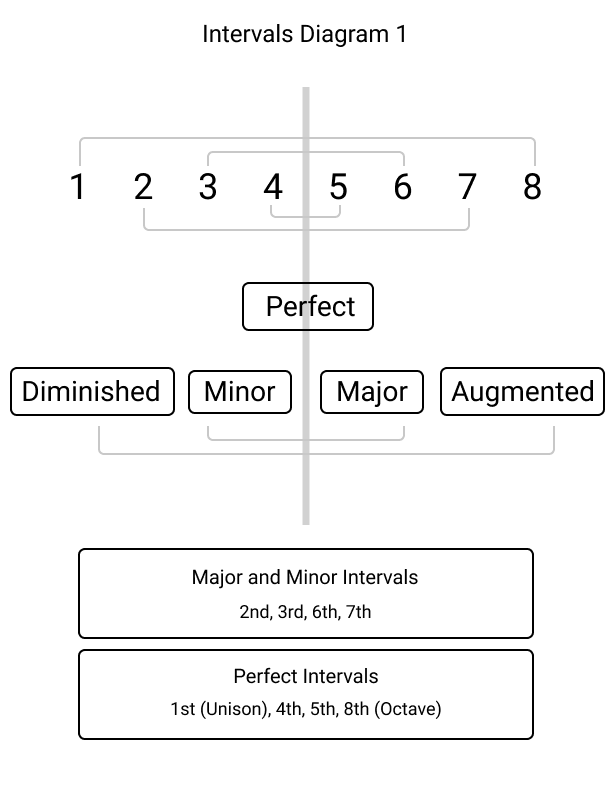
How the diagram works
Let me explain piece by piece. When they come together, it will make sense. First, see the vertical line in the middle of the diagram? That's the line we use to flip the intervals.
Next, look at the numbers with brackets. The numbers refer to the intervals, and the brackets show that those numbers can be flipped. For instance, an interval of 2nd and 7th can be flipped, same with a 3rd and 6th. You can flip them because the quality of the sound is very similar when they are flipped. A 3rd and 6th sound similar, a 4th and 5th sound similar in quality.
Next, you see 'Perfect', 'Diminished', and so on. Just like the interval numbers, minor and major can be flipped, same for the diminished and augmented. We haven't talked about diminished and augmented intervals yet, so for now, if you know that those terms exist, that is all you need to know.
Below that, it shows major and minor intervals, as well as perfect intervals which, you are quite familiar with now.
Let's flip intervals!
All right, let's flip some intervals. Try flipping a minor 3rd. Along the vertical line, minor and major can be flipped, and 3rd and 6th can be flipped. So when you flip a minor 3rd, it will become a major 6th.
Let's do some more. Try a perfect 5th. A perfect interval stays perfect when you flip it. 5th and 4th can be flipped. So when you flip a perfect 5th, it will become a perfect 4th.
Okay, one more. Let's flip a major 2nd. Major becomes minor, and 2nd becomes 7th, so the answer is minor 7th.
This flipping method becomes handy when you need to figure out large intervals, like 7th. For instance, when you see C# to B, it may startle you a little. Well then, let's flip it. Go from B to C#, that is a major 2nd. So when you flip it back, the original interval should be a minor 7th.
You can also flip intervals to double check your answer. Say, you think this interval is a minor 6th. Flip it and see if it will become a major 3rd. If it does, you guessed right.
There is one more thing I want to mention. Look at the numbers again. You will notice that when you add the two numbers that can be flipped with each other, it always becomes 9. 1+8 = 9, 3+6 = 9, and so on. In other words, when you flip the interval, you subtract the number from 9, and you get the answer. For instance, when you flip an interval of a 2nd, it will be a 7th (9-2 = 7). This is yet another way you can figure out intervals.
Now that we have learned major, minor, and perfect intervals, let's move onto augmented intervals!